
It is a fact that Russia has many talented mathematicians. Just look at the lists of mathematics olympiad winners or at the International Collegiate Programming Contest - Russian last names come up more often than others. But how has this come about? And has it always been the case?
Until the second quarter of the 18th century, higher mathematics did not arouse much interest in Russia - even polymath Mikhail Lomonosov was not familiar with it. It was Peter the Great who changed the situation: In 1724, the Emperor founded the St. Petersburg Academy of Sciences, and in 1725, issued a decree inviting “learned people” to the new institution and “providing necessary allowances to those who wish to come to Russia.” Russian envoys went head-hunting and succeeded spectacularly: The most promising minds of the time, including outstanding Swiss mathematicians Leonhard Euler and Daniel Bernoulli, moved to St. Petersburg.

Leonhard Euler (1707-1783) by Jakob Emanuel Handmann.
Deutsches Museum, MunichInitially, the new discipline failed to prosper - there were more professors than students, and they delivered lectures to one another. But the charisma and authority of the expats did their job: Mathematical sciences took root in our country, and by the 19th century, the Russian Empire had already produced its own mathematicians of the highest caliber.
The works of Euler and Bernoulli fell on fertile ground - the naturally paradoxical mentality typical of Russians was an excellent basis for the emergence of original mathematical theories and concepts. A national mathematical school and, with it, a system for teaching mathematics came into being. Its outstanding representatives in the 19th and early 20th centuries were the developer of applied aspects of mathematical analysis and theories of magnetism and probability, Mikhail Ostrogradsky; the founder of Russian demography, Viktor Bunyakovsky; and the first female professor of mathematics in the world, Sofya Kovalevskaya. But Nikolai Lobachevsky, one of the creators of non-Euclidean geometry, and Pafnuty Chebyshev, a generalist mathematician who made lots of fundamental discoveries, played a special role in the creation of the Russian school of mathematics.
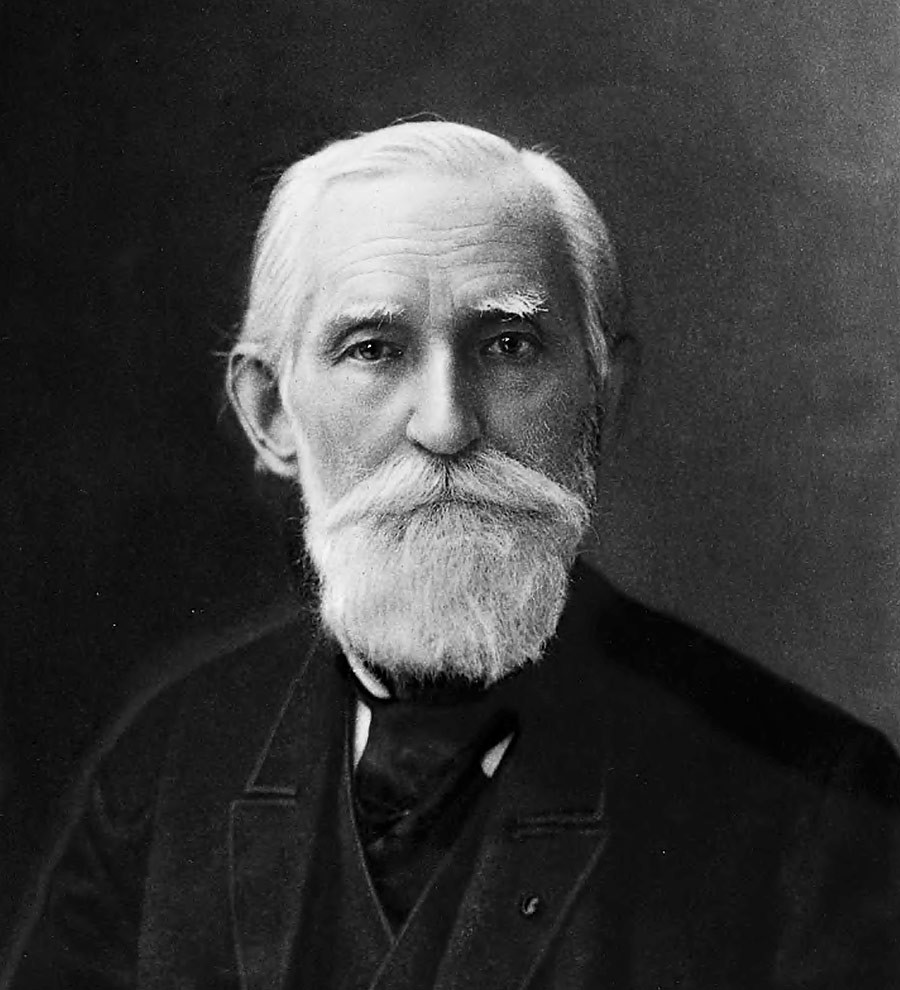
Pafnuty Chebyshev (1821–1894) was a prominent Russian mathematician, professor on algebra, number theory, and probability at St. Petersburg University and member of many Academies.
The History of Academy of Science of USSR / Nauka, 1964Their disciples and followers defined the development of Russian and global mathematical thought for a long period.
Following the 1917 Revolution, further scientific achievements were put in jeopardy: Many brilliant mathematicians left the Land of the Soviets. When he came to power, Stalin realized that it was strategically important to preserve the Russian mathematical school. A wave of “mathematical industrialization” swept the country - specialized educational and scientific centers were set up at a Stakhanovite pace. At first, the changes affected higher education - new universities were opened in Voronezh, Gorky, Perm, Sverdlovsk, Rostov and Irkutsk. Already in 1924, Soviet scientists excelled at the International Congress of Mathematicians, receiving several top awards. In the 1950s, at the initiative of Andrey Kolmogorov, an outstanding Soviet mathematician and one of the authors of probability theory, the system of mathematics education at school also underwent a reform: High-powered boarding schools specializing in physics and maths opened throughout the Soviet Union, embodying the ideals of the mathematics schools in Ancient Greece.

Andrey Kolmogorov at the 1973 Soviet Information Theory Symposium held in Tallinn.
Terrence L. FineThe results of these “mathematics construction projects” were not long in the making - nine laureates of the Fields Medal, two laureates of the Abel Prize, 10 winners of the Wolf Prize in Mathematics and three winners of the Clay Mathematics Institute prize, not to mention regular victories by our students at international mathematical olympiads.
After the collapse of the USSR, the boarding schools specializing in mathematics became the main exporters of high-class maths specialists to foreign countries. Having left the country, many graduates formed the scientific vanguard of top world universities and achieved outstanding results in programming. This “brain drain” was an illustration of the crisis in which Russian science and higher education found themselves in the 1990s, when an almost complete lack of state funding and of orders from industrial enterprises left talented mathematicians with little choice. But even in the West, our mathematicians maintained contact with the country of their birth and continued to maintain the image of Russia as one of the global “power centers” in mathematics.
In the early 2000s, the Russian economy rose from the ruins and Russian mathematical sciences underwent a renaissance. In 2002-2003, Grigori Perelman published works in which he proved the Poincaré conjecture, which the international mathematics community had been trying to solve since 1904. In 2010, our compatriot and author of numerous discoveries related to the scaling limits of two-dimensional lattice models, Stanislav Smirnov, was awarded the Fields Medal - the most prestigious such award in mathematics, which is presented to scientists aged under 40 for outstanding achievements.

Stanislav Smirnov.
Press photoIn the same year, Smirnov founded an advanced research laboratory at St. Petersburg State University (SPbGU), which was named after legendary Russian mathematician Pafnuty Chebyshev.
In today's Russia, the leading sectors of the economy - for instance, the oil industry, where no innovation is possible without fundamental research - devote more and more attention to young scientists. Thus, since 2013, the Chebyshev Laboratory has been supported by Gazprom Neft as part of the Rodnye Goroda social investment programme. Thanks to this cooperation, young mathematicians are now involved in creating digital oil field models and algorithms of analysis of large data arrays for calculating new oil reserves; and in September 2019, a new faculty of mathematics and computer sciences was opened at the SPbGU laboratory.

Students at the Chebyshev Laboratory.
Press photoAnother joint initiative by Gazprom Neft and the university is the Mathematical Progression project: Every year, for successful research material, university undergraduates and postgraduates receive company scholarships and grants. Some graduates who have been on the scheme have already joined the world mathematics elite: For example, after graduating from St. Petersburg University and working at the Chebyshev Laboratory, Aleksandr Logunov received a Clay Research Award - the second most prestigious prize in mathematics - and an invitation to become a professor at Princeton University.
If using any of Russia Beyond's content, partly or in full, always provide an active hyperlink to the original material.
Subscribe
to our newsletter!
Get the week's best stories straight to your inbox